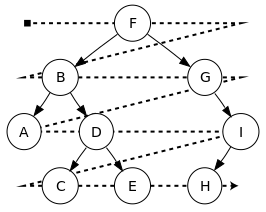
Binary Tree

Binary tree is called so because of its shape. It’s like a tree, it have leaves and a root. In computer science, the “tree” is usually upside down, the root at the top and leaves grow below it. It is binary so it every node only can have 0, 1 or 2 leaves.

Terminologies

Leaf Node

The node do NOT have any child nodes.

Inner Node

The Node between the leaf node and the root.

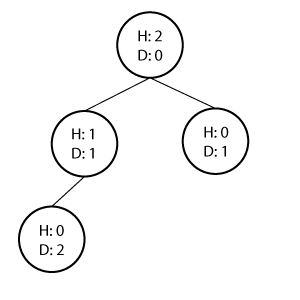
Height and Depth

Height and Depth of the tree are basically the same thing which indicates how many levels the tree have, usually starts at 0.

However, the height and depth of the node is different. The height and depth of a node is the distance on longest path to the leaf node and root respectively.

Types

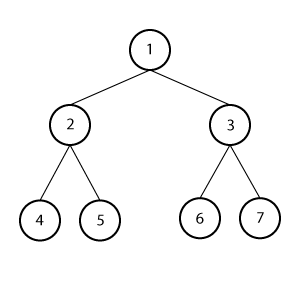
Full Binary Tree

Every node in the tree has either 0 or 2 children.

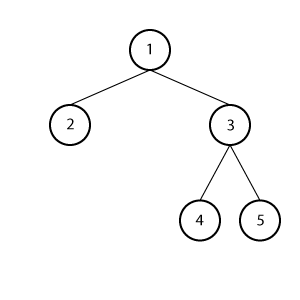
Complete Binary Tree

Every level except possibly the last level, has maximum number of nodes. All nodes in the last level are all at the left of the tree continuously.

Implementation

Array

Array can be used to store a tree, usually in breadth-first order. It is quite good at store a complete binary tree as it will not waste spaces. The root is store at the index \(i = 0\), and its children are stored in \(i = 1\) and \(i = 2\). It has property that A node at \(i\), its children at \(2i + 1\) (left) and \(2i + 2\) (right). However, it wastes a lot of spaces when storing other trees other than complete binary trees.

Struct or Class

Creating nodes and connect them to their parents.

1
2
3
4
5

struct node {
    int data;
    struct node* left;
    struct node* right;
}

Tree Traversal

Depth First Search (DFS)

Search the tree in the priority of depth. Using recursive calls for tree traversal is usually a good idea.

Pre-order

Root-Left-Right

1. Starts from the root
2. If left subtree has element in it, go to left. If not, go right.

In-order

Left-Root-Right

Post-order

Left-Right-Root

Determine a unique tree

There are only two ways to determine a unique tree given two types of traverse order.

Pre-order and In-order

The first element of a pre-order must be the root of the tree. Then find the same element in the In-order, we can divide the tree into two subtrees, left and right. Using the length of the left and right subtrees to find the sequences in pre-order respectively, then we can find the root element for left and right subtrees. Recursive repeat this process.

In-order and Post-order

Similar as above, except the root element is the last element in post-order traversal.

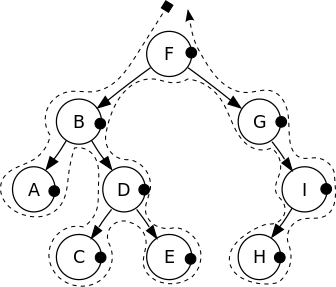
Tips

Rather than remembering the sequence, there is another way to remembering the order.

1. Draw a continuous line, starts and ends at the root of the tree, starts from left, around the tree
2. Try following:

• Pre-order: draw a dot at the left of each node
• In-order: draw a dot at the bottom of each node
• Post-order: draw a dot at the right of each node

1. Follow the line we drew, the sequence of touching dots is the sequence of traversal.

Pre-order	In-order	Post-order

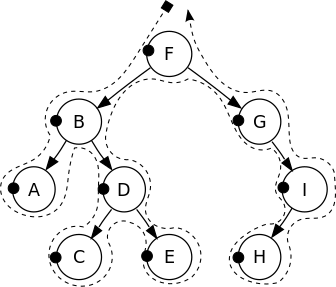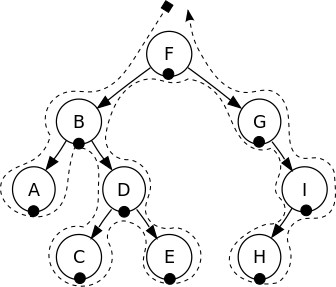Breadth First Search (BFS)

Traverse from the root to bottom, go thought each level first.