UVa 108 Maximum Sum

Given an array with size \(N \times N (N \le 100)\), find the maximum value of its subarray.

Link: Problem on UVa

Solutions

First thought is to brute force - find all possible subarrays then the time complexity will be \(O(N^6)\). TLE for sure.

Then comes up with an algorithm that takes \(O(N^4)\), which is enough to AC.

However, it can be \(O(N^3)\), see solution 2.

Solution 1

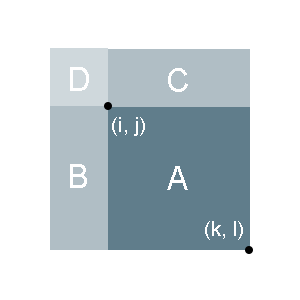
We build a sum array which is the sum of the numbers in rectangle area with the top-left of the array and bottom-right node \(i, j)\).

Then as we can see at the graph below, it is obvious that $$ \begin{align} A &= (A+B+C+D)\\ &-(B+D)\\ &-(C+D)\\ &+D \end{align} $$ Therefore we have A = sum[k][l] - sum[i-1][l] - sum[j-1][k] + sum[i-1][j-1]. Go through every subarray to find the maximum.

There is a trick that store the array starts with index 1 and initialize 0. So you don’t need to do boundary check. Stuck at first, could not figure out why and then found that I used < instead of <= in the for loop.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include<iostream>
#include<algorithm>
#define maxn 100+5
using namespace std;
int v, N, sum[maxn][maxn] = {{0}};

void solve() {
	int MaxSum = -200;

	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) {
			for (int k = i; k <= N; k++) {
				for (int l = j; l <= N; l++) {
					MaxSum = max(MaxSum, sum[k][l]-sum[i-1][l]-sum[k][j-1]+sum[i-1][j-1]);
				}
			}
		}
	}
	cout << MaxSum << endl;
}

int main(void) {
	while(cin >> N) {
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= N; j++) {
				cin >> v;
				sum[i][j] = v+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
			}
		}

		solve();
	}

	return 0;
}

Solution 2

In one dimension, if we want to find the maximum sum of successive elements, we have equation: $$ d[k] = max(d[k-1]+d[k], d[k])$$ There is a small improvement. By using greedy, we know if the sum is less than 0, there is no point to “add” it, we can just discard it.

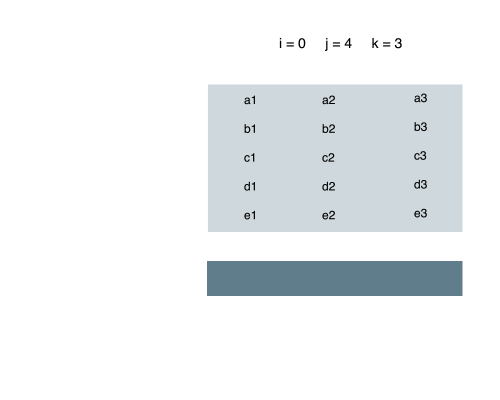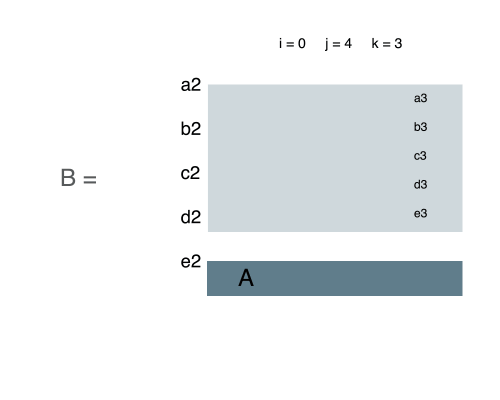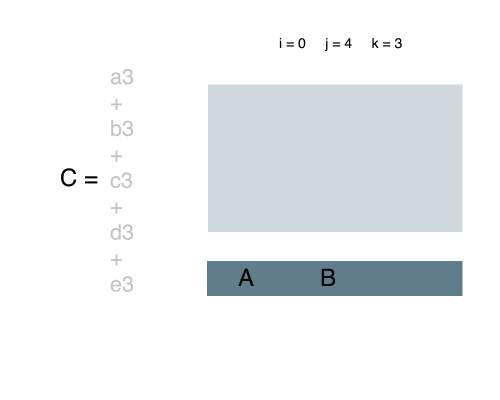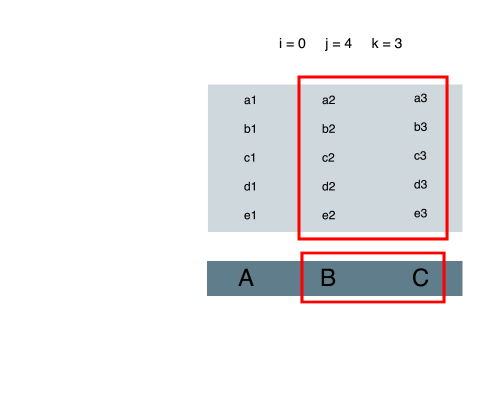
After we know how to compute in one dimension, it is easy to do it in two dimension.

Let

i = the starting line
j = the ending line, where i <= j
k = the number of columns

We can compress all lines between i and j into a 1D array. In other words, add each number in the same column together and put it in the 1D array. Hence, we have an array with i to j lines in it.

Now, it is just the problem we have already seen. Find the maximum sum of successive elements in the 1D array. That is the sum of the whole rectangle in the original 2D array.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 100+5
using namespace std;
int N, m[maxn][maxn], x[maxn];

int find_max() {
	int cur_sum=x[0], sum=0;
	for (int l = 0; l < N; l++) {
		sum += x[l];
		cur_sum = max(sum, cur_sum);
		if (sum < 0) sum = 0;
	}
	return cur_sum;
}

void solve() {
	int MaxSum = -200;
	for (int i = 0; i < N; i++) {
		memset(x, 0, sizeof(x));
		for (int j = i; j < N; j++) {
			for (int k = 0; k < N; k++) x[k] += m[j][k];
			MaxSum = max(MaxSum, find_max());
		}
	}
	cout << MaxSum << endl;
}

int main(void) {
	while(cin >> N) {
		for (int i = 0; i < N; i++)
			for (int j = 0; j < N; j++)
				cin >> m[i][j];
		solve();
	}

	return 0;
}