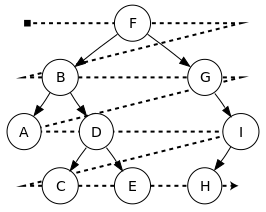
二叉树

二叉树之所以叫二叉树，是因为它每一个节点都至多有两个叉，又形似一棵树。树有根，有枝，有叶，只不过一般我们在计算机中所说的树都是根在上，叶在下的。

关于树的名词

叶节点

没有任何子节点的节点。

内节点

在根节点和叶节点中间的节点。

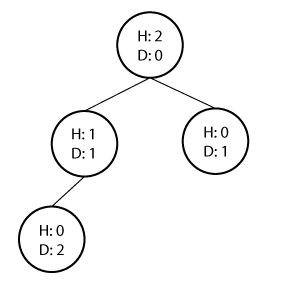
高度和深度

树的高度和深度指的都是该树有多少层，一般从0开始数。

但是，节点的高度和深度所指的就不同了。节点的高度是指该节点到叶节点的最长距离，节点的深度是指该节点到根节点的最长距离。

二叉树类型

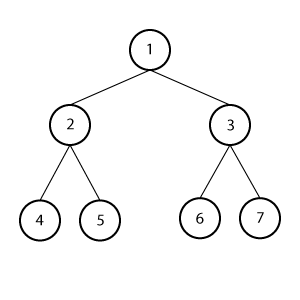
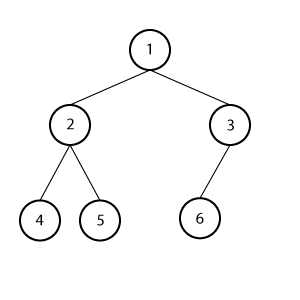
满二叉树

每个节点都有0或2个字子节点的树。

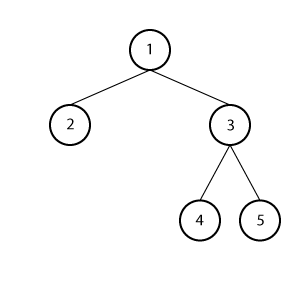
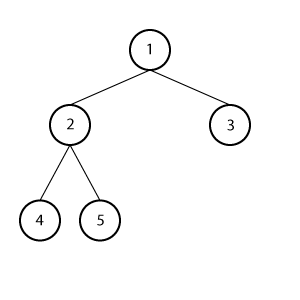
完全二叉树

一棵深度为\(h\)的树，除了第\(h\)层外，其他各层节点都为最大树，第\(h\)层的所有节点都连续地集中在左边。

实现

数组

树可以用数组来存储，一般是广度优先的顺序。数组可以很好地储存完全二叉树，因为完全二叉树不会浪费数组的空间。一般来说，根节点一般储存在\(i = 0\), 它的子节点存在\(i = 1\)和\(i = 2\)，分别代表左节点和右节点。一个节点在\(i\), 它的左右节点分别在\(2i + 1\)和\(2i+2\)。但是，数组会浪费很多空间如果树不完全。

Struct 或者 Class

创建节点，与父节点关联。

1
2
3
4
5

struct node {
    int data;
    struct node* left;
    struct node* right;
}

树的遍历

深度优先遍历(DFS)

遍历树按照深度优先的原则，使用递归一般在遍历中是个好主意。

先序遍历

根节点－左节点－右节点

1. 从根节点开始
2. 如果左子树有元素，遍历左子树，不然遍历右子树。

中序遍历

左－根－右

后序遍历

左－右－根

确定唯一的树

给定两种遍历顺序，只有两种方法能确定唯一的树。

先序遍历和中序遍历

先序遍历的第一个元素必定是树的根节点，在中序遍历中找到该节点，就能把树分为两个子树，左子树和右子树。根据左右子树的长度在先序遍历中找到对应的序列，便找到了左右子树的根节点。不断递归直到遍历树。

中序遍历和后序遍历

和上面说的类似，只是后序遍历的根节点在序列的最后。

小技巧

还有另外一种办法来记住遍历的顺序

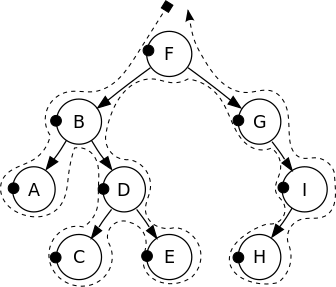
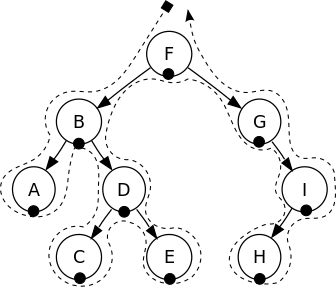
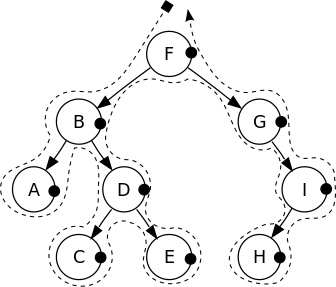
1. 画一条连续的线（一笔画），从根节点开始，往左画，包围整棵树，贴着节点，在根节点结束。
2. 类别：
   • 先序：在每个节点的左边画一个点
   • 中序：在每个节点的下面画一个点
   • 后序：在每个节点的右边画一个点
3. 从根节点开始，沿着画线的顺序，碰到点的顺序就是遍历的顺序。

先序遍历	中序遍历	后序遍历

广度优先遍历(BFS)

从根节点开始，以遍历完每一层为优先原则。