静态链表（链式前向星）- 表示图的另一种方法

静态链表是一种用数组静态储存的数据结构。它通常用来表示图。它还有个非常有趣的名字叫“链式前向星”。你可以通过以下两种方式来了解它：

• 从前向星开始.

• 从领接表开始.

但是我还是建议两种都了解一下啦。如果你知道其中一种或两种的吧，点这里跳过。点一下，玩一年。

在本文中，让u表示边从该节点出发，v表示边到达该节点。

前向星

前向星也叫做领接数组，边集数组。我们先把所有的边按照出发节点排序，到达节点的顺序不重要。接着分别用两个数组，一个存节点的在边数组的下标，一个存改节点的出度（有多少条边从该节点出发）。

范例

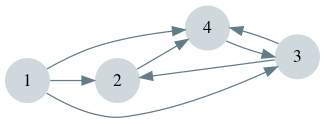
我们的图包含如下这些边（出，入）：

1
2
3
4
5
6
7

(1, 2)
(2, 4)
(3, 4)
(1, 3)
(4, 3)
(3, 2)
(1, 4)

我们首先以出发节点进行排序然后填入数组：

• es[]: 所有的到达节点

• head[]: 以u为起点的第一条边的位置

• len[]: u的出度（从该节点出发的边的数量）

1
2
3
4
5
6
7
8
9

(1, 2) --|
(1, 3) --| => len[1] = 3
(1, 4) --|
(2, 4)
(3, 2) => head[3] = 5
(3, 4)
(4, 3)
    ^
  es[]

下面我们来看如何取得所有从节点1出发的所有边。我们可以用head[1] == 1来找到第一条边在es[]中的位置是1。然后从head[1]到head[1]+len[1]遍历es[]，得到es[1+0] == 2, es[1+1] == 3, es[1+2] == 4。这样我们就得到了边(1,2), (1,3), (1,4)。

1
2
3
4

// 找到所有从u出发的边
for (int i = 0; i < len[u]; i++) {
    cout << u << " " << es[head[u]+i] << endl;
}

因为前向星需要进行一次排序操作，时间复杂度提升到了$ O(E \times log(E)) $， 所以前向星并不是非常常用。然而链式前向星避免了排序，就解决了这个问题。

领接表

领接表在C++中通常用vector<int> G[MAXN_V]来实现。G[u]指向一个包含所有从u出发的边的vector。

范例

最后的结果如下图所示，左边的数组表示G[]。当我们读入一条从u出发的边，就推入G[u]的vector.

1
2
3

for (int i = 0; i < G[u].size(); i++) {
    cout << u << " " << G[u][i] << endl;
}

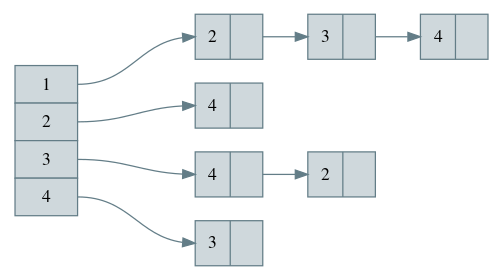
链式前向星

链式前向星是前向星的改进版本，也可以说是领接表的静态版本。它不用像前向星那样进行排序。它是怎么做到的？不停地戳自己！：）

范例

我们和上文使用相同的范例。

有如下边（出发，到达）：

1
2
3
4
5
6
7
8
9

(1, 2)
(2, 4)
(3, 4)
(1, 3)
(4, 3)
(3, 2)
(1, 4)
    ^
   es[]

我们开始构造数组：

• es[]: 所有的到达节点v，出发节点的信息会在head[]中储存。

• head[]: 以u为起点的第一条边的位置。

• next[]: 下一条以u为起点的边在es[]中的位置。用0来代表已经是最后一条了。

可以得到

我们需要另一个数组储存每个节点最后一条边的位置来构造next[]数组。当然我们也可以反向构造，不断更新head[]来储存。

下面我们来看如何得到从节点1出发的所有边：

1. 用head[1] == 1来找到第一条边的位置，设i = head[1]，es[i] == 2输出了(1, 2)这条边，更新 i = next[i]，现在i == 4。

2. es[i] == 3 输出边(1, 3)，更新i = next[i]，现在i == 7。

3. es[i] == 4 输出边(1, 4)，更新i = next[i], 现在i == 0。

4. 因为i == 0，结束。

1
2
3

for (int i = head[u]; i; i = next[i]) {
    cout << u << " " << es[i] << endl;
}

发现了吗？链式前向星除了第一次使用head[]，其他时候都在es[]和next[]之间左右横跳来得到下一数据。想法和链表很像，不过用的是数组实现的。

比较

前向星$O(E \times log(E))$的复杂度让人望而却步，有时候可能会变得更糟。

领接表易于理解，用C++ STL vector也易于实践。vector动态分配空间所以我们不用知道边的数量。但是，有时候可能会浪费空间因为vector在需要的时候会加倍分配空间。

链式前向星不改变数组的顺序，它只是建立起了边之间的关系。它比使用STL更快而且在理解之后易于实现。

但是，这些数据结构都在寻找一条特定的边的时候不太优秀，在最坏情况下需要遍历到链表结束。