UVa 108 Maximum Sum

Mar 24 2016 次阅读

给定一个$N \times N (N \le 100)$的矩阵，找到最大子矩阵和。

链接：题目UVa

题解

首先想到暴力，复杂度$O(N^6)$，肯定超时。

然后有一种$O(N^4)$的解法，AC足够了。

但是可以通过把二维矩阵压到一维，复杂度$O(N^3)$的解。看题解2哟。

题解 1

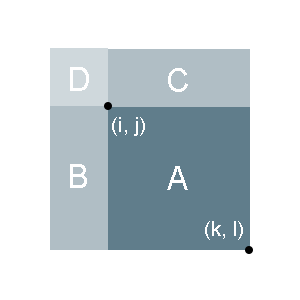
用数组sum保存自原矩阵左上角到右下角坐标为$i, j)$该区域内所有数的和。

如下图所示，显然有 $$ \begin{align} A &= (A+B+C+D)\\ &-(B+D)\\ &-(C+D)\\ &+D \end{align} $$ 所以我们可以得到 A = sum[k][l] - sum[i-1][l] - sum[j-1][k] + sum[i-1][j-1]。

有个小技巧，保存数组从 index 1 开始，初始化数组为 0 。这样可以省略边界处理。一开始样例都调不出来，找不到原因。后来发现我在 for 循环里用了 < 而不是 <=.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
#include<algorithm>
#define maxn 100+5
using namespace std;
int v, N, sum[maxn][maxn] = {{0}};

void solve() {
	int MaxSum = -200;

	for (int i = 1; i <= N; i++) {
		for (int j = 1; j <= N; j++) {
			for (int k = i; k <= N; k++) {
				for (int l = j; l <= N; l++) {
					MaxSum = max(MaxSum, sum[k][l]-sum[i-1][l]-sum[k][j-1]+sum[i-1][j-1]);
				}
			}
		}
	}
	cout << MaxSum << endl;
}

int main(void) {
	while(cin >> N) {
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= N; j++) {
				cin >> v;
				sum[i][j] = v+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
			}
		}

		solve();
	}

	return 0;
}

题解 2

在一维矩阵中，如果我们要找最大连续的区间和，状态转移方程如下： $$ d[k] = max(d[k-1]+d[k], d[k])$$ 有一个小优化就是根据贪心，我们知道如果当前的和小于0，就没有再使用它的意义了。因为加一个小于零的数肯定会减小和。

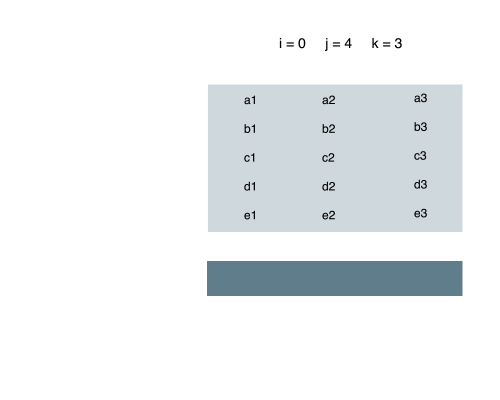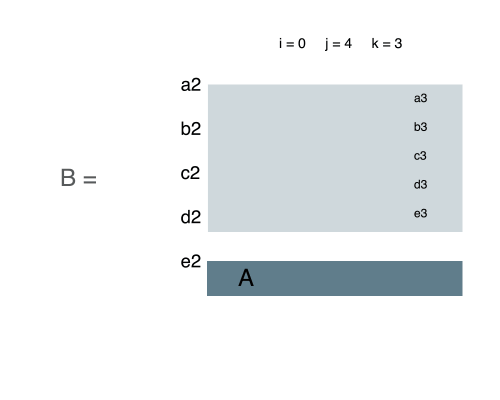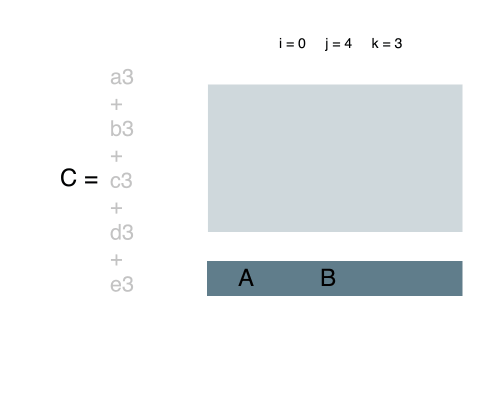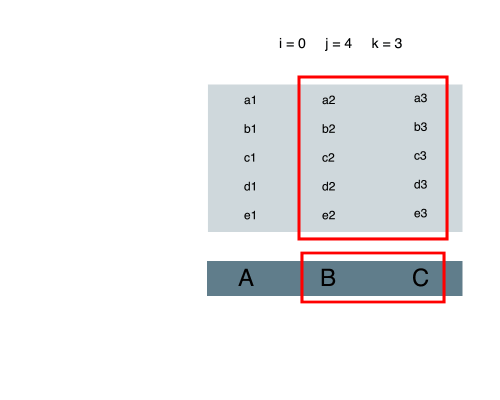
当我们知道了如何在一维中寻找最大连续区间的和，在二维中就很容易了。

设

i = 开始行数
j = 结束行数，有i <= j
k = 列数

我们可以把在 i 和 j 之间的所有行，以列的方式相加，储存到一维数组相应的角标下。

这样，这题就变成了一维数组求最大连续区间和了。找到的该和就是原二维数组中的长方形内所有数字的和。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 100+5
using namespace std;
int N, m[maxn][maxn], x[maxn];

int find_max() {
	int cur_sum=x[0], sum=0;
	for (int l = 0; l < N; l++) {
		sum += x[l];
		cur_sum = max(sum, cur_sum);
		if (sum < 0) sum = 0;
	}
	return cur_sum;
}

void solve() {
	int MaxSum = -200;
	for (int i = 0; i < N; i++) {
		memset(x, 0, sizeof(x));
		for (int j = i; j < N; j++) {
			for (int k = 0; k < N; k++) x[k] += m[j][k];
			MaxSum = max(MaxSum, find_max());
		}
	}
	cout << MaxSum << endl;
}

int main(void) {
	while(cin >> N) {
		for (int i = 0; i < N; i++)
			for (int j = 0; j < N; j++)
				cin >> m[i][j];
		solve();
	}

	return 0;
}

目录

UVa 108 Maximum Sum

题解

题解 1

题解 2